Algebra of Functions

Overview

• Section 2.6 in the textbook:
– Operations on Functions
– Difference Quotient
– Composition of Functions

Operations on Functions

• Functions can be added, subtracted,
multiplied, and divided to yield new
functions
– Given two functions f(x) and g(x)
  • Sum: (f + g)(x) = f(x) + g(x)
  • Difference: (f – g)(x) = f(x) – g(x)
  • Product: (f · g)(x) = f(x) · g(x)
  • Quotient: (f / g)(x) = f(x) / g(x), g(x) ≠ 0

• Given two functions f(x) and g(x):
– The domain of their sum, difference, or
product is the intersection of the domains of
f(x) & g(x)
– The domain of their quotient is the
intersection of the domains of f(x) & g(x)
EXCLUDING those values of x such that
g(x) = 0

Operations on Functions (Example)

Ex 1: Let f(x) = x + 1 and g(x) = x^2 + x – 2, find:

a) f(x) + g(x) and then (f + g)(3)
b) f(x) – g(x)
c) f(x) · g(x)
d) f(x) / g(x)
Also, find the domain for each

Operations on Functions (Example)

Ex 2: Let 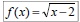and g(x) = x – 7, find:
f(x) / g(x) and its domain

Difference Quotient

• Given a function f, 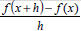is called the
difference quotient
– Allows us to study how f changes as we allow x to
vary
– You will see this again if you take Calculus
– For this class, just be able to calculate the difference
quotient and leave it in simplest form

Difference Quotient (Example)

Ex 3: Find the difference quotient of each
function

a) f(x) = 2x^2 – 3x + 1
b) f(x) = 5x – 2

Composition of Functions

• Given two functions f and g, the
composition of f and g is when g is used
as the input to f
–Written as (f ◦ g)(x) = f(g(x))
• This is NOT the same as f · g which is the product
– The domain of f ◦ g is the intersection of the
domain of g(x) and the domain of f(g(x))

Composition of Functions
(Example)

Ex 4: Let f(x) = 2x – 7 and 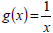, find:
a) (f ◦ g)(x)
b) (g ◦ f)(x)
c) (f ◦ f)(x)
Also, find the domain of each

Ex 5: Let 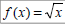and 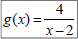, find:
a) (f ◦ g)(x)
b) (g ◦ f)(x)
Also, find the domain of each

Evaluating a Composition of
Functions

• To evaluate (f ◦ g)(a):
– Method I:
  • Compute (f ◦ g)(x)
  • Substitute x = a into the composition and evaluate
– Method II:
  • Compute b = g(a)
  • Compute f(b)

Evaluating a Composition of
Functions (Example)

Ex 6: Let f(x) = 4x + 3 and
g(x) = 3x^2 + x – 6, find:
a) (f ◦ g)(2)
b) (g ◦ f)(-1)
c) (f ◦ f)(½)

Summary

• After studying these slides, you should know
how to do the following:
– Add, subtract, multiply, or divide functions and
determine the domain of the new function
– Compute the difference quotient for a function
– Compute the composition of functions and be able to
compute its domain
– Evaluate a composition
• Additional Practice
– See the list of suggested problems for 2.6
• Next lesson
– Remainder & Factor Theorems (Section 3.1)