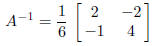Basic Matrix Operations
1. Let A = (aij) be an m × n matrix:
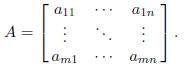
2. The transpose of A is the n × m matrix
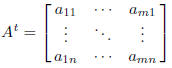
The rows of A are the columns of At. For example, if

then
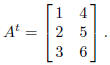
Note that (At)t = A.
3. If c is a scalar (i.e. a real or complex number) and A = (aij )is an m × n
matrix, then cA is the m × n
matrix with entries caij . So if A is given by (1) and c = 2, then
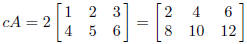
4. If A = (aij) and B = (bij) are m × n matrices, then the sum A + B is the m
× n matrix with entries
aij + bij . So if A is given by (1) and
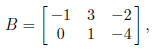
then
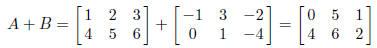
5. If A is an m × n matrix and B is n × k, then the product AB is the m × k
matrix whose ijth entry is
the dot product of the ith row of A and the jth column of B. For example, let

Since A is 2 × 3 and B 3 × 3, the product AB will be a 2 × 3 matrix. In particular,
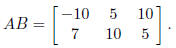
6. The m×m identity matrix Im is the m×m matrix with main diagonal entries 1
and 0’s everywhere else.
So, for example,
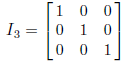
7. An m × m matrix A is invertible, or nonsingular if there is an m × m matrix A−1 such that
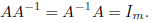
The matrix A−1 is called the inverse of A.
8. The determinant of the 2 × 2 matrix
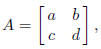
is
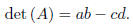
If det(A) ≠ 0, then A is invertible, and its inverse is
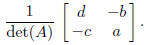
Since the matrix
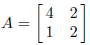
has det(A) = 6, it is invertible and