Solving Systems by the Method of Elimination

Addition Property of Equality (version 2): If a = b and c = d, then a + c = b + d.

•Systems of Two Linear Equations

Since systems of equations involve to sets of things that are equal we may add the equations together to give one new equation. If we do this in a way that eliminates one of the variables, then we'll be able to solve for the remaining variable.

 •Examples

Example 1:

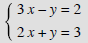
Solution: If we add these equations together we'll get a new equation that can be solved for x.

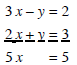
Now we can solve this and get x = 1. To get y we'll substitute into one of the original equations and solve.

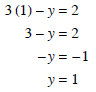
So the solution is (1,1).

Example 2:

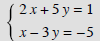
Solution: Adding these equations together won't eliminate a variable. To fix this problem we'll multiply the second equation by -2 to get the new system below.

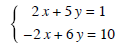
Now we can add these together.

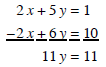
Solving this we get y = 1. Now we can find x.

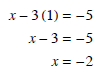
So the solution is (-2,1).

Example 3:

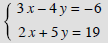
Solution: We can multiply the first equation by 2 and the second equation by -3, so that x will be eliminated. This gives the new system below.

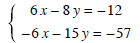
Now we can add and get the equation.

-23 y = -69

Solving this gives y = 3. Now we can find x.

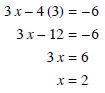
So the solution is (2,3).

Example 4:

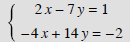
Solution: We can multiply the first equation by 2 and we get the following equations.

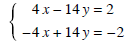
Adding these together we get 0 = 0 (or we can recognize that they are the same equation) and so there are infinite solutions.

Example 5:

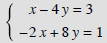
Solution: We can multiply the first equation by 2 and we get the following

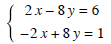
Adding these together we get 0 = 7, which is impossible, so there are no solutions.