Line Drawing
Line Drawing
Scan-Conversion Algorithms
• Scan-Conversion:
Computing pixel
coordinates for
ideal line on
2D raster grid
• Pixels best
visualized as circles/
dots
– Why? Monitor hardware
Drawing a Line
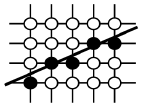
• y = mx + B
• m = Δy / Δx
• Start at leftmost x and increment by 1
→ Δx = 1
• yi = Round(mxi + B)
• This is expensive and inefficient
• Since Δx = 1, yi+1 = yi + m
– No more multiplication!
• This leads to an incremental algorithm
Digital Differential Analyzer
(DDA)
• If |slope| is less then 1
Δx = 1
else Δy = 1
• Check for vertical line
m = ∞
• Compute corresponding
Δy (Δx) = m (1/m)
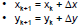
• Round (x,y) for pixel location
• Issue: Would like to avoid
floating point operations
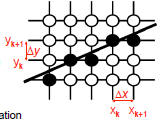
Generalizing DDA
• If |slope| is less than or equal to 1
– Ending point should be right of starting
point
• If |slope| is greater than 1
– Ending point should be above starting
point
• Vertical line is a special case
Δx = 0
Bresenham’s Algorithm
• 1965 @ IBM
• Basic Idea:
– Only integer
arithmetic
– Incremental
• Consider the implicit
equation for a line:
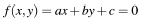
The Algorithm

Assumptions: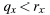
0 ≤ slope ≤ 1
Pre-computed: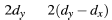
Bresenham’s Algorithm
Given:
implicit line equation:
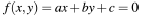
Let:
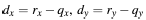
where r and q are points on the line and
dx ,dy are positive
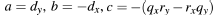
Then:
Observe that all of these are integers
and:
f(x,y) < 0 for points above the line
f(x,y) > 0
for points below the line
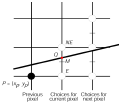
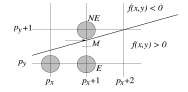
Now…..
• Suppose we just
finished (px,py)
– (assume 0 ≤ slope ≤ 1)
other cases symmetric
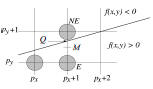
• Which pixel next?
– E or NE
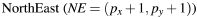
Assume:
• Q = exact y value at x = px + 1
• y midway between E and NE: M = py + 1/2
Observe:
If
Q < M , then pick E
Else pick NE
If
Q = M,
it doesn’t matter
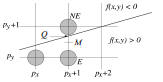
• Create “modified” implicit function (2x)
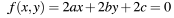
• Create a decision variable D to select,
where D is the value of f at the midpoint:
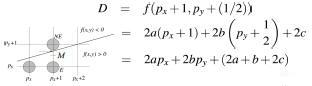
• If D > 0then M is below the line f(x,y)
– NE is the closest pixel
• If D ≤ 0then M is above the line f(x,y)
– E is the closest pixel
• Note: because we multiplied by 2x, D is
now an integer---which is very good news
• How do we make this incremental??


