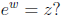THE MATHEMATICS OF STRING THEORY

1. Complex Numbers

1.1. The problem with reality. In calculus, most of the functions that you considered
had both domain and range contained in the real numbers R. The real numbers are good for
most real-life purposes, and we can describe most everything in the world around us using
real numbers. However, if we are interested in the algebra of polynomials, we soon run into
a problem. Given a polynomial p(x) with real coe cients, such as p(x) = x² - 1, one of the
things we can do is factor it.

x² - 1 = (x + 1)(x - 1)

into linear or rst order polynomials. If we factor a polynomial as

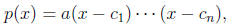
the values 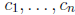are called the roots or zeroes of the polynomial, because p(c_i) = 0 for
each i = 1, . . . , n. Equivalently, they are the solutions of the polynomial equation p(x) = 0.

The problem with the real numbers is when we consider a polynomial such as p(x) = x²+1.
It cannot be factored using real numbers, and the equation x² + 1 = 0, or equivalently
x² = -1, has no real solutions. This is because a negative number has no real square root.
More generally, if we consider quadratic polynomials of the form p(x) = ax² + bx + c, recall
that the roots are given by the quadratic equation.

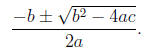
We have a problem if the discriminant b² - 4ac is negative, since then we cannot take the
square root, and the quadratic polynomial has no real roots.

To work around this problem, we introduce a new type of number, called the imaginary
numbers which are the square roots of negative real numbers. In particular, if we let
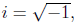
then all imaginary numbers are just real multiples of i. For instance, we compute

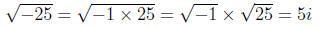
and

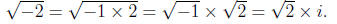
Taking the real and imaginary numbers together, we obtain the complex numbers.

Definition 1.1. The complex numbers are numbers of the form.

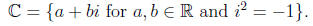
Using the complex numbers, we can factor every quadratic polynomial using the quadratic
formula. In fact, we can do much more.

Theorem 1.2 (Fundamental Theorem of Algebra). Every polynomial with complex coefficients
 (and in particular, every polynomial with real coefficients, since the real numbers are
contained in the complex numbers with imaginary part 0) can be completely factored as a
product of linear polynomials.

A number system satisfying this property, that every polynomial can be completely fac-
tored into linear polynomials, is called algebraically complete.

1.2. Complex arithmetic. In order to understand the complex numbers, we must describe
how the normal arithmetic operations of addition and multiplication work in C. We follow
the normal rules of algebra, treating i as an unknown variable, but substituting i² = -1.
We have.

(a + bi) + (c + di) = (a + c) + (b + d)i

and

(a + bi) (c + di) = a c + bi c + a di + bi di = (ac - bd) + (bc + ad)i.

How do we subtract complex numbers? That's easy. We just add the negative (or additive
inverse) of the complex number.

-(a + bi) = -a + (-b)i.

How do we divide complex numbers? That's rather harder. We must first find the reciprocal
(or multiplicative inverse) of a complex number. To do that, we introduce the complex
conjugate.

if z = a + bi, then 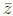= a - bi,

obtained by flipping the sign of the imaginary part only. The complex conjugate is useful
since multiplying a complex number by its conjugate gives us

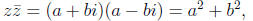
which is a real number with no imaginary part. In fact 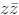is a non-negative real number,
and 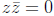only if both a = 0 and b = 0. We are now able to compute the reciprocal, as

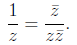
Example 1.3. Here we divide

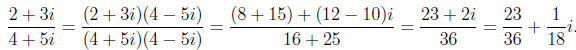
Note that we can also use the complex conjugate to extract the real and imaginary parts
of a complex number, as follows.

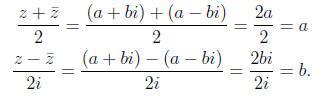
1.3. Geometric interpretation. One of the most interesting features of the complex num-
bers is that they can be viewed as points in the two dimensional xy plane by identifying the
complex number z = a + bi with the point with coordinates (x, y) = (a, b). In fact, they
are better viewed not just as points but rather as displacements or vectors. A vector can be
thought of as an arrow starting at the origin (0, 0) and ending at a particular point. The
advantage of thinking of complex numbers as vectors is that two vectors are added by placing
their arrows end to end, and constructing a new arrow from the origin to the destination.
(This is basically the two dimensional version of how you were taught to add using a number
line.) This vector addition corresponds precisely to the addition of complex numbers.

There is also a geometric interpretation of multiplication, although for that we need to
use polar coordinates. Recall that the the polar coordinates for a point in the plane
are given by

&bull,its modulus r is the distance from the origin, and we usually take r≥,0.
•,its angle θ, formed between the point (or, more precisely, its vector) and the positive
real axis, measured counterclockwise, and we usually

Given a complex number z = a + bi, the modulus is given by

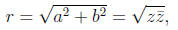
and the angle is given by

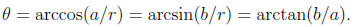
Using polar coordinates, a complex number can be written in the form

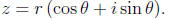
Given another complex number also written in polar coordinates,

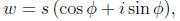
their product is given by

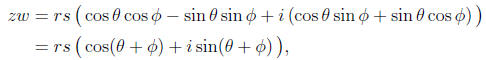
where we observe that our formula for the product of two complex numbers corresponds to
the angle addition formulae for sin and cos. So, taking the product of two complex numbers
multiplies their moduli and adds their angles.

Using polar coordinates, we can also take powers of complex numbers. Given a complex
number 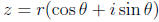, then its nth power is

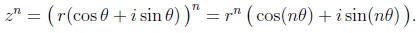
In addition, we can take fractional powers, or roots, of complex numbers. For instance, a
square root of a complex number is given by

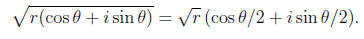
There is no problem taking 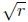since r≥,0. We get the second square root (minus the first)
by replacing the original angle θ, with the equivalent angle

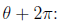
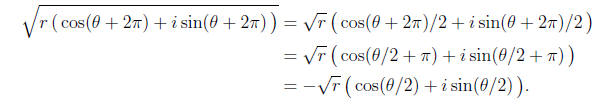
In general, a nonzero complex number has a total of n nth roots, given by starting with the
original angle θ,, as well as taking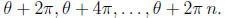

1.4. Euler's formula. The mathematician Leonhard Euler discovered a beautiful identity.

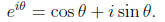
We can show why this is true using Taylor series. We have

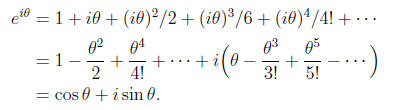
In particular, Euler noted his famous formula

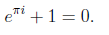
Using this exponential notation, our polar coordinate formula for the product of two complex
numbers becomes

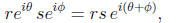
which follows from the identity 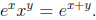Also, the formula for the powers of a complex
number is simply

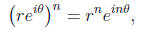
which follows from the identity 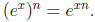In the particular case of n = -1, the reciprocal
of a complex number is

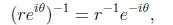
taking the reciprocal of the modulus and the negative of the angle.
Using this exponential notation, the complex conjugate of 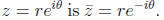Extracting
the real and complex parts of 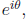we obtain the formulae.

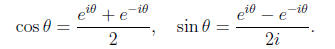
1.5. Exercises.
(1) Write the complex fraction 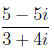in the form a + bi.

(2) In the complex numbers, the number -1 has two square roots, i. Compute the
three cube roots of -1. Write each of them both in exponential form and in the form
a + bi.

(3) Write the number 1 - i in exponential form, and compute (1 - i)⁴.

(4) What can you say about the logarithm of a complex number? In other words, given
a complex number z, what complex number or numbers w satisfy