Section 5-3: Factoring Trinomials of the Form1x² ± bx ± c

The FOIL process changes a product of 2 binomials into a polynomial. The reverse process starts
with a polynomial and finds the 2 binomials whose product will be that polynomial. The process of
changing a polynomial into a product of 2 binomials is called factoring a polynomial. This unit will
look at factoring two types of trinomials.

A second degree Trinomial that has1x^2 as the first term and ends with a positive number.

A second degree Trinomial that has1x^2 as the first term ends with a negative number.

The technique for factoring each type of trinomial is similar. We will start with the first type.

Factoring Trinomials that start with a1x^2 and
end with a positive last term into(x ± a ) (x ± b)

The results of the FOIL of (x + 5) (x + 3) i s a trinomial with a first, middle and last term.

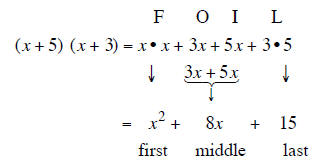
The First Term of the trinomial is x ^2 . This first term comes from the products of the two first terms
of the binomials(first₁ ± last₁) (first₁ ± last ₂ ). The only way get a product of x ^2 in the trinomial is to
have both first terms of the binomials be x. (x __ ) (x __ )

The Last Term of the trinomial is positive 15. It comes from the product of the two last terms of
of the binomials (x ± last₁ ) (x ± last ₂) . If the last term of the trinomial is positive 15 then the last two
terms in the binomials (x ± last₁) (x ± last₂ ) could be +3 and +5 or -3 and -5 but we don't know
which one to use.

In either case when you FOIL the two middle terms of the trinomial will have the same signs and the
middle term of the trinomial will be found by adding the two last terms of the binomials.

The Middle Term of the trinomial is + 8. It comes from adding the last two terms of the binomials
(x ± last₁) (x ± last₂ ). Only the +3 and +5 add to give +8 s so the last two terms in the binomials
must be +3 and +5.

The binomials whose product is x ^2 + 8x +15 must be (x + 3) (x + 5) so
(x + 3) (x + 5) are the factors of x ^2 + 8x +15
Factoring trinomials that start with a 1x^2 and end with a with a positive last term into (x ± a ) (x ± b)

Example 1

Factor x^2 + 10x + 24 into (x ± a ) (x ± b)

The two last terms of (x ± last₁) (x ± last₂ ) must multiply to give 24 and add to give +10

Step 1: The only two first terms that multiply to give x^2 are x and x. Put them in the first places in
both of the parenthesis.

Step 2: List all the ways the last term can be multiplied to give 24.

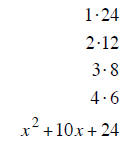
Step 3: Find the pair of products that will Add to give + 10. (+ 4 and + 6 work)

Step 4: Put these two terms into the last places in the parenthesis. (x + 4) (x +6)

Step 5: Check your answer by FOIL.

Example 2

Factor x ^2 −11x + 30 into (x ± a ) (x ± b)

The two last terms of (x ± last₁) (x ± last₂ ) must multiply to give 30 and add to give –11

Step 1: The only two first terms that multiply to give x^2 are x and x. Put them in the first places in
both of the parenthesis.

Step 2: List all the ways the last term can be multiplied to give 30.

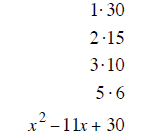
Step 3: Find the pair of products that will Add to give – 11 (– 5 and – 6 work)

Step 4: Put these two terms into the last places in the parenthesis. (x −5) (x − 6)

Step 5: Check your answer by FOIL.

Factoring trinomials that start with a 1x^2 and end with a with a positive last term into (x ± a ) (x ± b)

Example 1	Example 2	Example 3
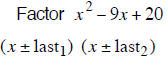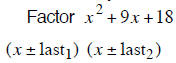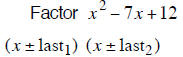last terms must multiply to 20	last terms must multiply to 18	last terms must multiply to 12
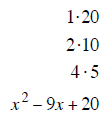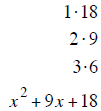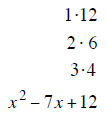last terms must add to – 9	last terms must add to + 9	last terms must add to –7
–4 and –5 add to – 9	+ 3 and + 6 add to + 9	–3 and –4 add to –7
(x − 4) (x −5)	(x + 3) (x + 6)	(x − 3) (x − 4)

Example 4	Example 5	Example 6
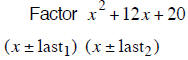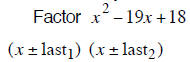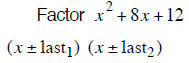last terms must multiply to 20	last terms must multiply to 18	last terms must multiply to 12
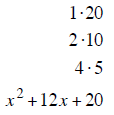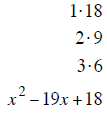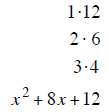last terms must add to +12	last terms must add to – 19	last terms must add to + 8
+ 2 and + 10 add to + 12	– 1 and – 18 add to – 19	+ 2 and + 6 add to + 8
(x + 2) (x +10)	(x −1) (x −18)	(x + 2) (x + 6)

Example 7	Example 8	Example 9
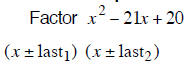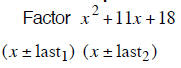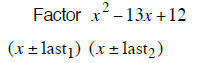last terms must multiply to 20	last terms must multiply to 18	last terms must multiply to 12
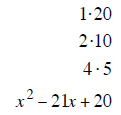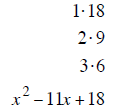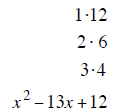last terms must add to – 21	last terms must add to +11	last terms must add to –13
– 1 and – 20 add to – 21	+ 2 and + 9 add to +11	–1 and –12 add to –13
(x −1) (x −20)	(x + 2) (x + 9)	(x −1) (x −12)

Factoring Trinomials that start with a 1x^2 and
end with a negative last term into (x ± a ) (x ± b)

The last section discussed how to factor Trinomials with a positive last term like x ^2 + 8x +15
The rules for factoring Trinomials with a positive last term were
1. The product of the last terms in (x ± last₁) (x ± last₂ ) must be +15
2. The sum of the last terms in (x ± last₁) (x ± last₂ ) must be –8

The rules for Factoring Trinomials with a negative last term are similar

Factoring Trinomials: Factor x ^2 − 2x −15 into (x ± a ) (x ± b) .

To determine a rule for finding a and b we FOIL (x − b)(x + a) to get

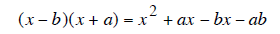
using the distributive property on the middle terms we get

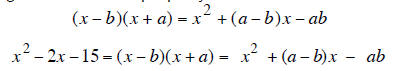
The First Term of the trinomial is x ^2 . This first term comes from the products of the two first terms
of the binomials (first₁ ± last₁) (first₁ ± last ₂ ). The only way get a product of x ^2 in the trinomial is to
have both first terms of the binomials be x. (x __ ) (x __ )

The Last Term of the trinomial is negative 15. It comes from the product of the two last terms of
of the binomials (x ± last₁ ) (x ± last ₂) . If the last term of the trinomial is negative 15 then the two last
terms in the binomials (x ± last₁) (x ± last₂ ) could be +3 and –5 or –3 and ≠5 but we don't know
which one to use.

In either case when you FOIL the two middle terms of the trinomial will have different signs and the
middle term of the trinomial will be found by subtracting the two last terms of the binomials.

The Middle Term of the trinomial is –2. It comes from subtracting the last two terms of the
binomials (x ± last₁) (x ± last₂ ). Only the +3 and –5 subtract to give –8 s so the two last terms in
the binomials must be +3 and –5.

The binomials whose product is x ^2 − 2x −15 must be (x + 3) (x − 5)
(x + 3) (x − 5) are the factors of x ^2 − 2x −15

Factoring trinomials that start with a 1x^2 and end with a with a negative last term