Parabolas Tutorial

Section 6.1: Parabolas

Learning Objectives:
1. Graph parabolas in which the vertex is the
origin.
2. Find the equation of a parabola.
3. Graph parabolas in which the vertex is not
the origin.
4. Solve applied problems involving
parabolas.

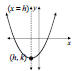
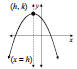
1. The Parabola

Parabolas that Open Up or Down
The graph of y = a(x – h)² + k or y = ax² + bx + c is a parabola that
1. opens up if a > 0 and opens down if a < 0.
2. has vertex (h, k) if the equation is of the form y = a(x – h)²+ k.
3. has a vertex whose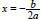

coordinate is The y-coordinate
is found by evaluating the equation at the x-coordinate of the
vertex

y = a(x – h)² + k, a > 0

y = a(x – h)² + k, a < 0

1. The Parabola

A parabola is the collection of all points P in the plane that are
the same distance from a fixed point F as they are from a fixed
line D. The point F is called the focus of the parabola, and the
line D is its directrix. In other words, a parabola is a set of points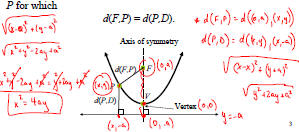

2. Equations of a Parabola

From the distance formula we can obtain the fact that the equation
of the parabola whose vertex is at the origin and opens to the right is
y² = 4ax.

Equations of a Parabola: Vertex at (0, 0); Focus on an Axis; a > 0
Vertex	Focus	Directrix	Equation	Description
(0, 0)	(a, 0)	x = – a	y² = 4ax	Parabola, axis of symmetry is the x-axis; opens to the right
(0, 0)	(– a , 0)	x = a	y² = – 4ax	Parabola, axis of symmetry is the x-axis; opens to the left
(0, 0)	(0, a)	y = – a	x² = 4ay	Parabola, axis of symmetry is the y-axis; opens up
(0, 0)	(0, – a)	y = a	x² = – 4ay	Parabola, axis of symmetry is the y-axis; opens down

Graphing a Parabola

Example continued: Graph the equation x² = – 16y.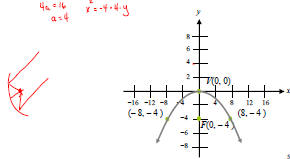

Finding the Equation of a Parabola

Example: Find an equation of the parabola with vertex at (0, 0)
and focus at (– 8, 0).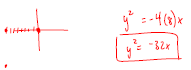

3. A Parabola Whose Vertex is Not the Origin

Parabolas with Vertex at (h, k); Axis of Symmetry Parallel to a Coordinate Axis, a > 0
Vertex	Focus	Directrix	Equation	Description
(h, k)	(h + a, k)	x = h – a	(y – k)² = 4a(x – h)	Parabola, axis of symmetry parallel to x-axis; opens to the right
(h, k)	(h – a, k)	x = h + a	(y – k)² = – 4a(x – h)	Parabola, axis of symmetry parallel to x-axis; opens to the left
(h, k)	(h, k + a)	y = k – a	(x – h)² = 4a(y – k)	Parabola, axis of symmetry parallel to y-axis; opens up
(h, k)	(h, k – a	y = k + a	(x – h)² = – 4a(y – k)	Parabola, axis of symmetry parallel to y-axis; opens down

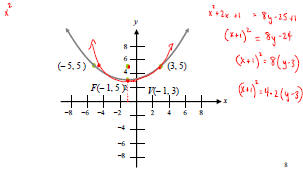
A Parabola Whose Vertex is Not the Origin

Example continued: Graph the parabola x² + 2x – 8y + 25 = 0.

Home