College Algebra Syllabus

NUMBER: Math 1414

COURSE TITLE: College Algebra

CREDIT HOURS:

4 LECTURE HOURS: 4
LAB HOURS: 0
CLN/REC HOURS: 0

PREREQUISITE: Math 1332 or TSI placement.

COREQUISITE: None

TEXTBOOK:

College Algebra, Custom Edition, available in August Only at Collin’s
bookstores.

SUPPLIES: Graphing calculator required

COURSE DESCRIPTION:

Relations and functions: linear, polynomial, rational, exponential, logarithmic and inverse functions,
composition of functions, absolute value, theory and systems of equations, complex numbers,
matrices, sequences, and the binomial theorem.

COURSE MEASURABLE LEARNING OBJECTIVES:

Upon completion of this course the students should be able to do the following:

1. Analyze relations between variables
2. Classify and manipulate functions and their graphs
3. Find the zeros and factors of polynomials with real coefficients
4. Solve exponential and logarithmic equations with applications to growth and decay
5. Use matrices to solve systems of linear equations
6. Analyze sequences, including arithmetic and geometric sequences

COURSE REQUIREMENTS:

Attending class
Completing homework assignments
Completing labs
Completing required exams

COURSE FORMAT:

Lecture and guided practice.

METHOD OF EVALUATION:

A minimum of four written exams and a comprehensive final exam. Homework and/or quizzes may be
used in place of one exam or in addition to exams. The weight of each of these components of
evaluation will be specified in the individual instructor’s addendum to this syllabus. All out-of-class
course credit, including take-home exams, home assignments, service-learning, etc. may not exceed
25% of the total course grade; thus, at least 75% of a student’s grade must consist of exams given in
the class or testing center, and no student may retake any of these exams.

ATTENDANCE POLICY:

Attendance is expected of all students. If a student is unable to attend, it is his/her responsibility to
contact the instructor to obtain assignments. Please see the schedule of classes for the last day to
withdraw.

RELIGIOUS HOLY DAYS:

In accordance with section 51.911 of the Texas Education Code, the college will allow a student who
is absent from class for the observance of a religious holy day to take an examination or complete an
assignment scheduled for that day within a reasonable time. A copy of the state rules and procedures
regarding holy days and the form for notification of absence from each class under this provision are
available from the Admissions and Records Office.

COURSE REPEAT POLICY:

All students may repeat this course only once after receiving a grade, including W. For example
students who have taken this course twice have to choose a different course to take after two
trials.

ADA STATEMENT:

It is the policy of Collin County Community College to provide reasonable and appropriate
accommodations for individuals with documented disabilities. This College will adhere to all
applicable Federal and State laws, regulations and guidelines with respect to providing
reasonable accommodations as required to afford equal educational opportunity. It is the
student's responsibility to contact the ACCESS Office (G-200) or 972.881.5898, (TDD
972.881.5950) in a timely manner if he/she desires to arrange for accommodations.

ACADEMIC ETHICS:

The college may initiate disciplinary proceedings against a student accused of scholastic dishonesty.
Scholastic dishonesty includes, but is not limited to, statements, acts, or omissions related to
applications for enrollment or the award of a degree, and/or the submission of material as one’s own
work that is not one’s own. Scholastic dishonesty may involve one or more of the following acts:
cheating, plagiarism, collusion, and/or falsifying academic records

Cheating is the willful giving or receiving of information in an unauthorized manner during an
examination, illicitly obtaining examination questions in advance, using someone else’s work for
assignments as if it were one’s own, copying computer disks or files, and any other dishonest means of
attempting to fulfill the requirements of a course.

Plagiarism is the use of an author’s words or ideas as if they were one’ s own without giving credit to
the source, including, but not limited to, failure to acknowledge a direct quotation. Contact the Dean of
Students at 972.881.5771 for the student disciplinary process and procedures or consult the CCCCD
Student Handbook.

SPECIFIC REQUIREMENTS/COURSE CONTENT:

The student will be responsible for knowing all definition and statements of theorems for each section
outlined in the following modules.

Module 1

The student will be able to:

1. Evaluate functions including the Difference Quotient and Piecewise-Defined Functions.
2. Determine the domain and range of functions.
3. Determine intervals over which functions are increasing, decreasing, or constant.
4. Find relative maxima or minima of functions.
5. Determine if a function is even or odd from equations and graphs.
6. Graph common functions including linear, quadratic, cubic, square root, cube root, reciprocal,
absolute value, and piecewise-defined functions.
7. Interpret transformations on common functions such as shifts, reflections, stretches and shrinks.
8. Perform composition operations on functions.
9. Use the Horizontal Line Test to test for one-to-one functions.
10. Verify or find inverses of functions algebraically and graphically.
11. Write the equation of a line using the point-slope form. (Optional) Module 2 The student will be able to:
12. Write quadratic functions in standard form by completing the square. (Optional)
13. Sketch quadratic functions and state their vertex, axis of symmetry, and intercepts.
14. Solve application problems using parabolas.
15. Identify zeros of polynomials and their multiplicity.
16. Sketch graphs of polynomial functions.
17. Use synthetic division to find zeros and factors of polynomial functions.
18. Evaluate polynomial functions for given values using the Remainder Theorem.
19. Find complex zeros of polynomial functions.
20. Apply the Rational Zero Theorem.
21. Know that complex zeros occur in conjugate pairs.
22. Know the implications of the Fundamental Theorem of Algebra.
23. Know the implications of the Linear Factorization Theorem.
24. Determine the domain of rational functions.
25. Determine the vertical, horizontal, and oblique (slant) asymptotes of rational functions.
26. Solve polynomial and rational inequalities.

Module 3

The student will be able to:

27. Graph exponential and logarithmic functions including transformations.
28. State the domain, range and asymptotes of exponential and logarithmic functions.
29. Evaluate logarithms.
30. Use properties of logarithms.
31. Solve exponential and logarithmic equations.
32. Apply solution techniques to solve application problems relating to growth and decay.

Module 4

The student will be able to:

33. Convert systems of linear equations to matrix form.
34. Use Gauss-Jordan elimination to solve systems of linear equations with two and three variables
and equations by hand or using ROWOPS.
35. Use matrices to solve real life applications.
36. Find the determinant of 2 x 2 and 3 x 3 matrices without a calculator.
37. Use Cramer's Rule to solve systems of linear equations with two and three variables.
38. Write the terms of a sequence.
39. Use sigma notation for sums.
40. Determine the common difference of arithmetic sequences.
41. Find the formula for the 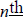term of arithmetic and geometric sequences.
42. Find the sum of the first n terms of arithmetic and geometric sequences.
43. Determine the common ratio of geometric sequences.
44. Find the sum of an infinite geometric series.