External Direct Products

We have the basic tools required to studied the
structure of groups through their subgroups and
their individual elements and by means of
isomorphisms between groups. This allows us to
build up larger groups from smaller ones.

Let 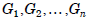be groups. Then the external
direct product of these groups, denoted
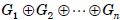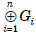or , is the set of all n-tuples
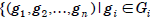for each i = 1, 2, … , n}.

Combining elements of this set under the
componentwise operations of the G_i’s makes their
external direct product a group. (Why?)

Examples:

• We are already very familiar with vector
addition in the groups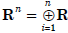

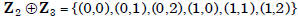• is a
cyclic group, generated by (1,1). The map from
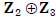to 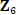defined by k(1,1) k is an
isomorphism between them (why?).

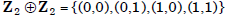• is not cyclic
(why?). Thus, 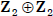and 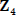are structurally
distinct groups.

Theorem The order of 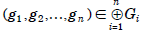is


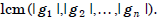
Proof The order of 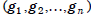is the smallest
exponent k for which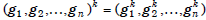
equals 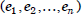. Thus, 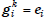for each i. So k is
a multiple of 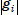for each i, and being the smallest
number with this property forces k to be exactly
//

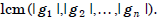Theorem If G and H are finite cyclic groups, then
G ⊕H is cyclic 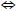|G| and |H| are relatively
prime.

Proof If |G|= m and |H|= n, then |G ⊕H|= mn.
So if G ⊕H is cyclic and has (g, h) as a generator,
then with d = gcd(m, n), we have

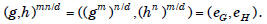
But then 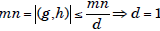. So m and n are
relatively prime. Conversely, if m and n are
relatively prime, then l (g,h) l= lcm(m, n) = mn,
whence (g, h) must be a generator for G ⊕H. //

Corollary If are finite cyclic groups,
then is cyclic the orders l G_i l are relatively
prime in pairs. //

Corollary 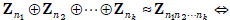the n_i’s
are relatively prime in pairs. //

(This last corollary is equivalent to an important
result in number theory which is known as the
Chinese Remainder Theorem and is often expressed
in terms of congruence arithmetic.)

Theorem If s and t are relatively prime, then
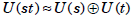. In fact, the subgroup



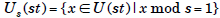
of U(st) is isomorphic to U(s), and similarly, the
subgroup .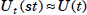

Proof We claim that the map from U(st) to
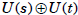given by 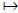(x mod s ,x mod t) is an
isomorphism. This follows from the claim that the
map from 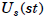to U(s) given by x 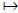x mod s is an
isomorphism. The details are omitted here. //

Corollary If the prime factorization of the integer
n is 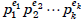(where the numbers p_i are distinct
prime numbers), then . //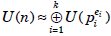

Gauss, in a work titled Disquisitiones Arithmeticae,
a monumental work in number theory published in
1801, proved results which we can interpret today
in the form of the following

Theorem U(2) is trivial; 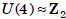; and for n > 2,
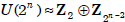. Moreover, for any odd prime p,


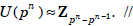
From Gauss’ theorem, it is possible to realize any
group of units U(n) as an external direct sum of
cyclic groups.

Example:



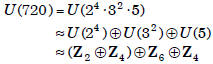
How many elements of order 12 are there in
U(720)? The same number as there are in
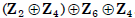. Viewing such an element in
the form (a, b, c, d), we note that this question now
takes the form

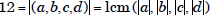
where

l a l= 1 or 2
l b l= 1, 2, or 4
l c l= 1, 2, 3, or 6
l d l= 1, 2, or 4

Given these options, c must equal 3 or 6 and one of
l b l  or l d l (or both) must equal 4. This gives three
cases:

(1) l a l= 1 or 2, l b l= 4, l c l = 3 or 6, l d l= 1 or 2;
(2) l a l= 1 or 2, l b l= 1 or 2, l c l= 3 or 6, l d l= 4;
(3) l a l= 1 or 2, l b l= 4, l c l= 3 or 6, l d l= 4.

Recalling that there are exactly φ (d) elements of
order d in a cyclic group, we can count the number
of elements of given orders in each of these
possibilities: there will be one element of orders 1
and 2, two elements of orders 3, 4 and 6. Putting
all this together gives in each case:

(1) (1 + 1)(2)(2 + 2)(1 + 1) = 32 elements;
(2) (1 + 1)(1 + 1)(2 + 2)(2) = 32 elements;
(3) (1 + 1)(2)(2 + 2)(2) = 32 elements;

for a total of 96 elements of order 12 in U(720).