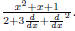Solving Differential Equations with Long Division
4.3 More manipulations
Just as the fraction
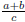can be decomposed into
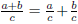, so can the fractions from differential
equations:
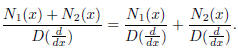
This is just stating that solutions to
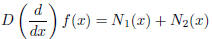
can be obtained by taking solutions from the equations
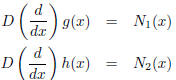
and adding them: f(x) = g(x) + h(x).
And this is just a generalization of the integration step,
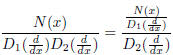
which says merely that a solution of
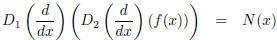
can be obtained by solving (in order)
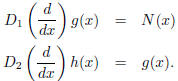
However, we won't have much need for this until we look at
more advanced stuff.
5 Putting it all together
We now have three rules, integration, exponential shift, and long division,
which combined give a powerful
means to tackle approximately half of the differential equations one faces in a
first class in differential
equations.
To summarize, when faced with a differential equation
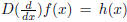and where
is some
constant coefficient polynomial in
and h(x) is some sum
of polynomials, exponentials, and polynomials
times exponentials, you can always find a sequence of steps and manipulations
which will arrive at one
solution.
Let's demonstrate with one complicated example. The differential equation is,
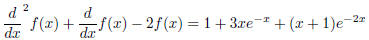
which means our fraction is
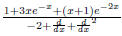
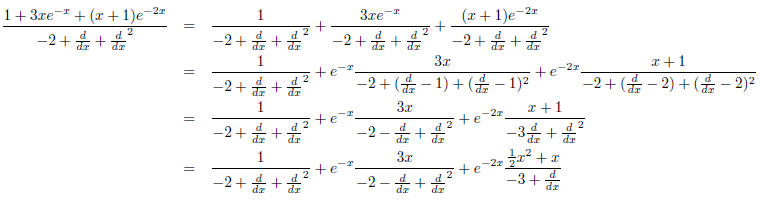
Doing long divisions,
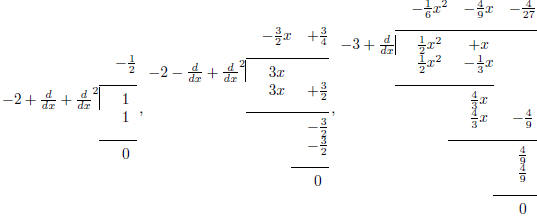
We arrive at a solution
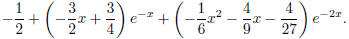
6 General solutions
The techniques shown so far will produce a solution to an important class
differential equations, but just as
in calculus, having one answer is not always enough. While
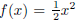is a solution of
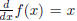there
are other solutions which all have the form
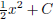where C is some constant, i.e. "any two
integrals differ
by no more than a constant".
When we solve differential equations, one or several integrations occur, and
getting the most general
solution is a matter of keeping track of the Cs that come from them.
With the differential equations we are studying, this notion of a constant that
solutions can differ by is
replaced with something more general. Say f1(x) and f2(x) are both solutions of
, i.e.
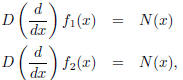
then, by subtracting the two equations, we have
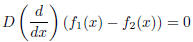
showing that two solutions differ by no more than a
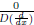solution. When trying to find just one
solution,
not caring which, we have taken
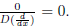Finding all possible solutions of
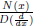amounts to finding one
solution of
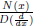and then adding to it all solutions of
.
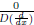Consider the example from integration,
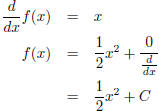
since C is the most general solution of
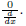This is what we already know about
indefinite integrals.
For a more complicated
we have to be
more clever.
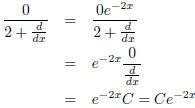
and we can check that
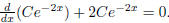Thus
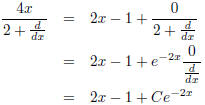
is the general solution. It is no coincidence that we took
0 to be
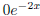in the above. If we had picked a
different exponential,
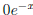, we would have gotten nowhere
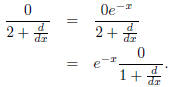
Finding the right exponential shifts to make the
s apparent requires a bit of trickery.
Lemma 6.1 (Roots of the denominator). If k is some number such that
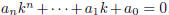, then
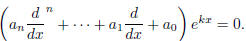
Conversely, the only solutions of
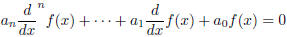
are of the form
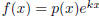where k D(k) = 0 and p(x) is a
polynomial with degree at most m where m
is the multiplicity of k in the factorization of D.
Proof.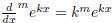
,so adding things
up we have
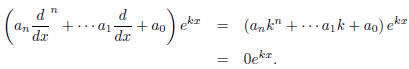
The converse is beyond the scope of this discussion.
In other words, to find all the solutions of
you need only consider those exponential shifts with
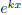
where D(k) = 0.
For example, k2 + k - 2 = 0 when k is either 1 or -2, so
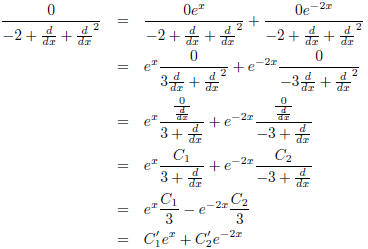
where
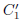and
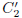are constants which "suck up" the 3s
and negative sign.
So what we have learned here is that to get general solutions, one has to find
all the solutions of
which come from exponential shifts that cause a
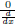(a.k.a. an unknown constant) to appear.
So the general solution to the large example problem is
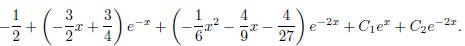
There are further simplifying tricks to finding all
solutions of
but you will have to
work those out
on your own.
7 Problems
Here are some differential equations to try things out on.
These only require long division.
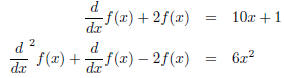
This requires long division and exponential shift.
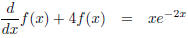
This requires all the tricks.
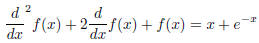
After you find one solution, you might want to try finding
the general solution (keeping track of the Cs).
When the highest derivative is
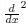there should be 2 of them and when the highest is
there should be 1.
7.1 Advanced
Show that if
is a polynomial
in
, and D(k) ≠ 0, then
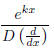
has the solution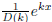
. An
easy way is to plug this into the differential equation. A more interesting way
is to use long division. What solutions can you find if D(k) = 0?
The polynomial k2 + 3k + 2 factors into (k + 1)(k + 2). Show that
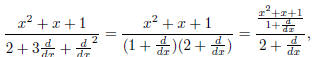
that is, first solve
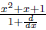and then take the result and "divide" it by
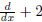and check to see that it is a
solution to
